Teil 1 – Einführung
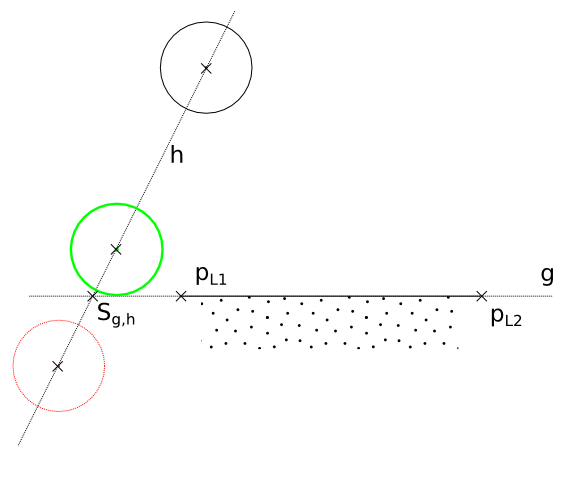
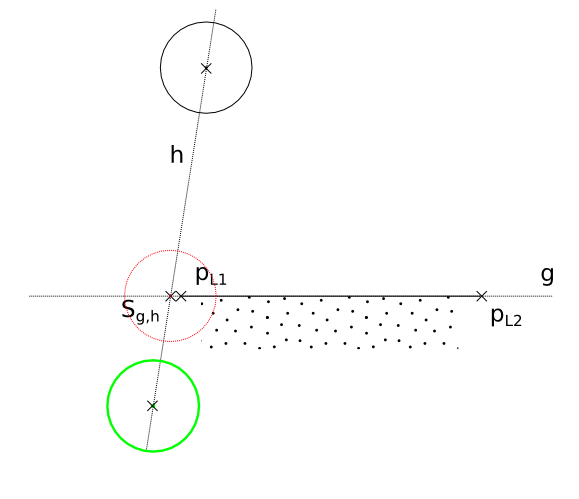
Teil 2 – Kollision mit Gerade
Teil 2 – Kollision mit Gerade – Demoprogramm
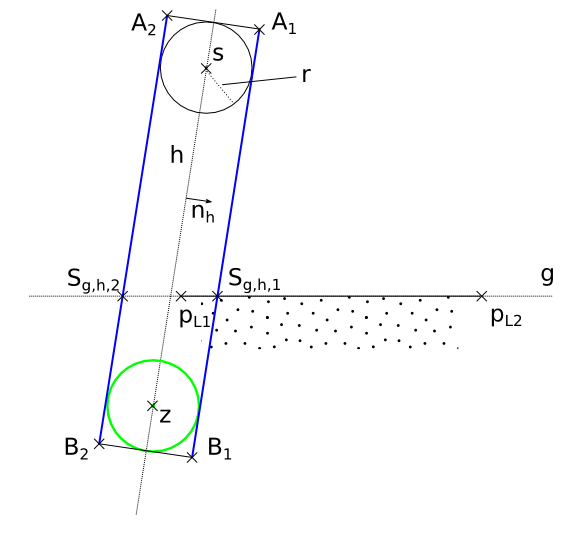
Teil 3 – Kollision mit Strecke
Teil 3 – Kollision mit Strecke – Demoprogramm
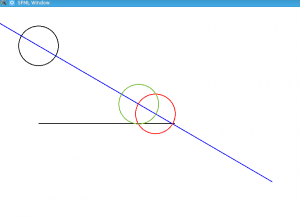
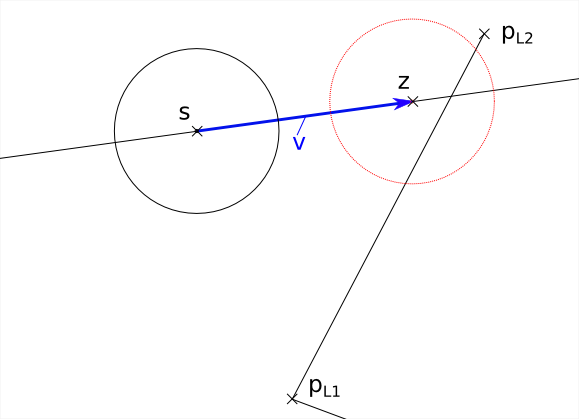
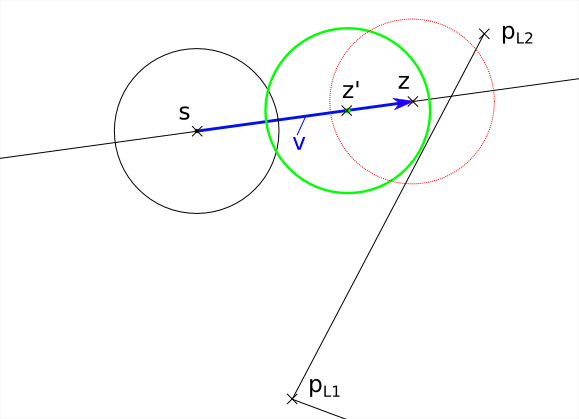
Zur Demonstration der bisherigen Lösung habe ich ein kleines Programm geschrieben, in welchem man sich die berechnete Lösung für beliebe Ausgangssituationen anzeigen lassen kann. Man sieht, dass nicht wirklich vorhandene Kollisionen nun nicht mehr fälschlicherweise „korrigiert“ werden.
Screenshot:

Bedienung :
Linke Maustaste, Drag&Drop : roter und schwarzer Kreis, Enden der schwarzen Linie
Rechte Maustaste, Drag&Drop : Bildschirmausschnitt
Mausrad : Zoomen
Ausprobieren: win-06.02.2011-21.09
Relevante Quellcodeausschnitte:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | bool TestBoundedMovement::DoLineSegmentsIntersect( sf::Vector2f s1, sf::Vector2f e1, sf::Vector2f s2, sf::Vector2f e2 ) { sf::Vector2f v1 = e1 - s1; sf::Vector2f v2 = e2 - s2; sf::Vector2f intersection; if ( LinesIntersection( s1, v1, s2, v2, intersection ) ) { float k = LineParam( s1, v1, intersection ); float m = LineParam( s2, v2, intersection ); if( ( m >= 0 ) && ( m <= 1 ) && ( k >= 0 ) && ( k <= 1 ) ) { return true; } else { return false; } } else return false; } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | bool TestBoundedMovement::LinesIntersection( sf::Vector2f s1, sf::Vector2f v1, sf::Vector2f s2, sf::Vector2f v2, sf::Vector2f &intersection ) { if( v1.x != 0 ) { float a = v2.x * v1.y / v1.x - v2.y; if( a != 0 ) { float m = ( s2.y - s1.y - ( s2.x - s1.x ) * v1.y / v1.x ) / a; intersection.x = s2.x + m * v2.x; intersection.y = s2.y + m * v2.y; return true; } else { return false; } } else { if ( v2.x != 0 ) { float m = ( s1.x - s2.x ) / v2.x; intersection.x = s2.x + m * v2.x; intersection.y = s2.y + m * v2.y; return true; } else { return false; } } } |
1 2 3 4 5 6 7 8 9 10 | float TestBoundedMovement::LineParam( sf::Vector2f s, sf::Vector2f v, sf::Vector2f p ) { float k = 0; if( v.y != 0 ) { k = (p.y - s.y) / v.y; } else if ( v.x != 0 ) { k = (p.x - s.x) / v.x; } return k ; } |
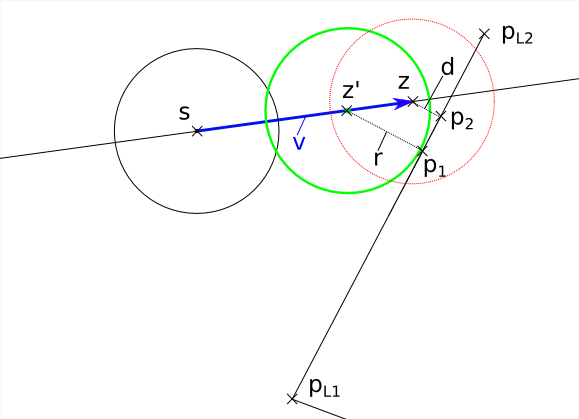
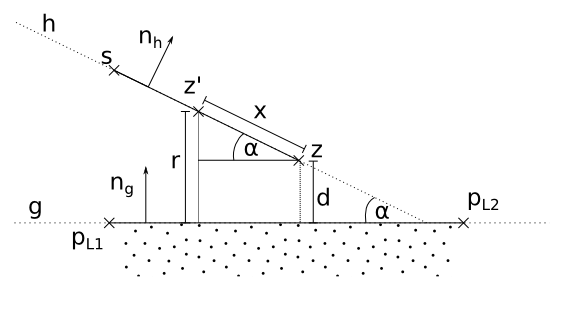
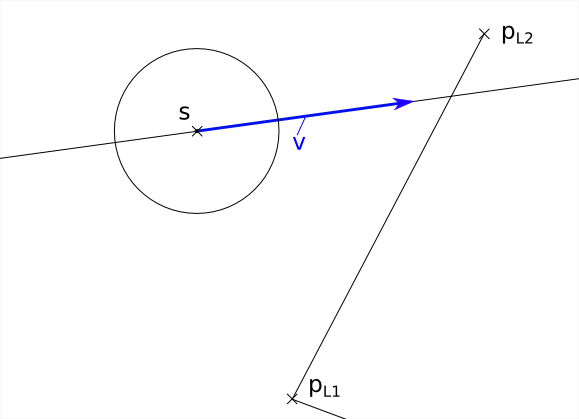
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 | void TestBoundedMovement::UpdateCorrectDest() { sf::Vector2f s = myCircleStart.GetPosition(); sf::Vector2f v = myVector; sf::Vector2f pl1 = myLineBound.GetP1(); sf::Vector2f pl2 = myLineBound.GetP2(); sf::Vector2f z = s + v; sf::Vector2f ng0; sf::Vector2f nh0; if ( MathUtils::VectorLen(v) == 0 ) { myCircleCorrectDest.SetPosition( z ); return; } sf::Vector2f v0 = v / MathUtils::VectorLen(v); if ( MathUtils::ComputeNormal( pl1, pl2, ng0 ) && MathUtils::ComputeNormal( s, z, nh0 ) ) { float r = radius; if( ! DoLineSegmentsIntersect( s + nh0 * r, z + v0 * r + nh0 * r, pl1, pl2 ) && ! DoLineSegmentsIntersect( s - nh0 * r, z + v0 * r - nh0 * r, pl1, pl2 ) && ! DoLineSegmentsIntersect( z + v0 * r + nh0 * r, z + v0 * r - nh0 * r, pl1, pl2 )) { //Bewegungslinie und BoundLine überschneiden sich nicht, //also wird keine Kollisionserkennung vorgenommen, //also ist myCircleCorrectDest = myCircleDest myCircleCorrectDest.SetPosition( z ); return; } if( MathUtils::DotProduct( v, ng0 ) > 0 ) { //Bewegungsvektor zeigt von BoundingLine weg, //also wird keine Kollisionserkennung vorgenommen, //also ist myCircleCorrectDest = myCircleDest myCircleCorrectDest.SetPosition( z ); return; } if( MathUtils::DotProduct( s - pl2, ng0 ) < 0 ) { //Der Startpunkt liegt hinter der Line //also wird keine Kollisionserkennung vorgenommen, //also ist myCircleCorrectDest = myCircleDest myCircleCorrectDest.SetPosition( z ); return; } float d = ( MathUtils::DotProduct( z - pl2, ng0 ) ); if( d >= r ) { //Es findet gar keine Kollision statt //also ist myCircleCorrectDest = myCircleDest myCircleCorrectDest.SetPosition( z ); return; } float cosAlpha = MathUtils::DotProduct( v, pl2 - pl1 ) / ( MathUtils::VectorLen( v ) * MathUtils::VectorLen( pl2 - pl1 ) ); float sinAlpha = sqrt( 1 - cosAlpha * cosAlpha ); if( sinAlpha != 0 ) { float x = ( r - d ) / sinAlpha; sf::Vector2f z2 = z - x * v0; myCircleCorrectDest.SetPosition( z2 ); } } else { //Normale konnte nicht berechnet werden, //also liegen pl1 und pl2 auf einem Punkt, //also ist BoundingLine nicht vorhanden, //also ist myCircleCorrectDest = myCircleDest myCircleCorrectDest.SetPosition( z ); } } |


 .
.